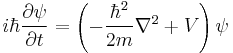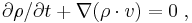Pilot wave

In theoretical physics, the Pilot Wave theory was the first known example of a hidden variable theory, presented by Louis de Broglie in 1927. Its more modern version, the Bohm interpretation, remains a controversial attempt to interpret quantum mechanics as a deterministic theory, avoiding troublesome notions such as instantaneous wavefunction collapse and the paradox of Schrödinger's cat.

Contents

The Pilot Wave theory

The Pilot Wave theory is one of several interpretations of Quantum Mechanics. It uses the same mathematics as other interpretations of quantum mechanics; consequently, it is also supported by the current experimental evidence to the same extent as the other interpretations.

Principles

The Pilot Wave theory is a hidden variable theory. Consequently:

The positions and momentums of the particles are considered to be the hidden variables. The observer doesn't know the precise value of these variables which introduces uncertainty into the theory.

A collection of particles has an associated matter wave, which evolves according to the Schrödinger Equation. Each particle follows a deterministic (but probably chaotic) trajectory, which is guided by the wave function; collectively, the density of the particles conform to the magnitude of the wave function. The wave function is not influenced by the particle and can exist also as an empty wave function.[1]

The theory has nonlocality, which makes it compatible with Bell's theorem.

Consequences

The Pilot Wave Theory shows that it is possible to have a realistic and deterministic hidden variable theory, which reproduces the experimental results of ordinary Quantum Mechanics. The price, which has to be paid for this is nonlocality.

Mathematical formulation for a single particle

The matter wave of de Broglie is described by the time dependent Schrödinger equation:

i \hbar \frac{\partial \psi}{\partial t} = \left( - \frac{\hbar^2}{2m} \nabla^2 %2BV \right)\psi \quad

The complex wavefunction can be represented as:

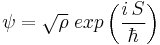
\psi = \sqrt{\rho} \; exp \left( \frac{i \, S}{\hbar} \right)

By plugging this into the Schrödinger-equation, one can derive two new equations for the real variables. The first is the continuity equation for the probability density \rho :

\partial \rho / \partial t %2B \nabla( \rho \cdot v) =0 \; ,

where the velocity field is defined by the guidance equation

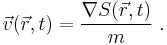
\vec{v} (\vec{r},t) = \frac{\nabla S(\vec{r},t)}{m}\; .

According to pilot wave theory, the point particle and the matter wave are both real and distinct physical entities. ( Unlike standard quantum mechanics, where particles and waves are considered to be the same entities, connected by wave-particle duality. ) The pilot wave guides the motion of the point particles as described by the guidance equation.

Ordinary quantum mechanics and pilot wave theory are based on the same partial diifferential equation. The main difference is that in ordinary quantum mechanics, the Schrödinger-equation is connected to reality by the Born postulate, which states that the probability density of the particle's position is given by 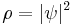\rho = |\psi|^2 . Pilot wave theory considers the guidance equation to be the fundamental law, and sees the Born rule as a derived concept.

The second equation is a modified Hamilton–Jacobi equation for the action S:

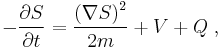
- \frac{\partial S}{\partial t} = \frac{\left(\nabla S\right)^2}{2m} %2B V %2BQ \; ,

where Q is the quantum potential defined by

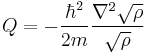
Q = - \frac{\hbar^2}{2m} \frac{\nabla^2 \sqrt{\rho}}{\sqrt{\rho}}

By neglecting Q, our equation is reduced to the Hamilton-Jacobi equation of a classical point particle. ( Stricly speaking, this is only a semiclassical limit, because the superposition principle still holds and one needs a decoherence mechanism to get rid of it. Interaction with the environment can provide this mechanism. ) So, the quantum potential is responsible for all the mysterious effects of quantum mechanics.

One can also combine the modified Hamilton-Jacobi equation with the guidance equation to derive a quasi-Newtonian equation of motion

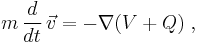
m \, \frac{d}{dt} \, \vec{v} = - \nabla( V %2B Q ) \; ,

where the hidrodynamic time derivate is defined as

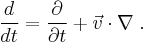
\frac{d}{dt} = \frac{ \partial }{ \partial t } %2B \vec{v} \cdot \nabla \; .

Mathematical formulation for multiple particles

The Schrödinger equation for the many-body wavefunction 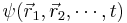\psi(\vec{r}_1, \vec{r}_2, \cdots, t) is given by

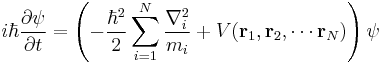
i \hbar \frac{\partial \psi}{\partial t} =\left( -\frac{\hbar^2}{2} \sum_{i=1}^{N} \frac{\nabla_i^2}{m_i} %2B V(\bold{r}_1,\bold{r}_2,\cdots\bold{r}_N) \right) \psi

The complex wavefunction can be represented as:

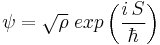
\psi = \sqrt{\rho} \; exp \left( \frac{i \, S}{\hbar} \right)

The pilot wave guides the motion of the particles. The guidance equation for the jth particle is:

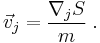
\vec{v}_j = \frac{\nabla_j S}{m}\; .

The velocity of the jth particle explicitly depends on the positions of the other particles. This means that the theory is nonlocal.

Empty wave function

Lucien Hardy[2] and J. S. Bell[1] have emphasized that in the de Broglie–Bohm picture of quantum mechanics there can exist empty waves, represented by wave functions propagating in space and time but not carrying energy or momentum,[3] and not associated with a particle. The same concept was called ghost waves (or “Gespensterfelder”, ghost fields) by Albert Einstein.[4]

The empty wave function notion has been discussed controversially.[5][6][7] In contrast, the many-worlds interpretation of quantum mechanics does not call for empty wave functions.[1]

History

In his 1926 paper,[8] Max Born suggested that the wave function of Schrödinger's wave equation represents the probability density of finding a particle.

From this idea, de Broglie developed the Pilot Wave theory, and worked out a function for the guiding wave. He presented the Pilot Wave theory at the 1927 Solvay Conference.[9] However, Wolfgang Pauli raised an objection to it at the conference, saying that it did not deal properly with the case of inelastic scattering. De Broglie was not able to find a response to this objection, and he and Born abandoned the pilot-wave approach.

Later, in 1932, John von Neumann published a paper claiming to prove that all hidden variable theories were impossible.[10] (A result found to be flawed by Grete Hermann three years later, though this went unnoticed by the physics community for over fifty years). However, in 1952, David Bohm, dissatisfied with the prevailing orthodoxy, rediscovered de Broglie's Pilot Wave theory. Bohm developed Pilot Wave Theory into what is now called the De Broglie-Bohm theory.[11]

The de Broglie-Bohm theory itself might have gone unnoticed by most physicists, if it had not been championed by John Bell, who also countered the objections to it. In 1987, John Bell[12] rediscovered Grete Hermann's work, and thus showed the physics community that Pauli's and von Neumann's objections really only showed that the Pilot Wave theory did not have locality; in fact, no quantum-mechanical theories have locality, so these objections did not invalidate the Pilot Wave theory.

The de Broglie-Bohm theory is now considered by some to be a valid challenge to the prevailing orthodoxy of the Copenhagen Interpretation, but it remains controversial.

Yves Couder and co-workers recently discovered a macroscopic pilot wave system in the form of walking droplets. This system exhibits behaviour of a pilot wave, heretofore considered to be reserved to microscopic phenomena.[13]

References

  1. ^ a b c J. S. Bell: Six possible worlds of quantum mechanics, Foundations of Physics, vol. 22, no. 10, Part I. Invited Papers Dedicated To Louis De Broglie, 1992, pp. 1201-1215, DOI: 10.1007/BF01889711, p. 1212
  2. ^ Lucien Hardy: On the existence of empty waves in quantum theory, Physics Letters A, vol. 167, no. 1, 6 July 1992, pp. 11-16, DOI: 10.1016/0375-9601(92)90618-V (abstract)
  3. ^ Franco Selleri, Alwyn Van der Merwe: Quantum paradoxes and physical reality, p. 86
  4. ^ Franco Selleri, Alwyn Van der Merwe: Quantum paradoxes and physical reality, Fundamental Theories of Physics, Kluwer Academic, 1990, ISBN 0-7923-0253-2, p. 85–86
  5. ^ Marek Zukowski: “On the existence of empty waves in quantum theory”: a comment, Physics Letters A, vol. 175, no. 3-4, 12 April 1993, pp. 257-258, DOI: 10.1016/0375-9601(93)90837-P (abstract)
  6. ^ H. D. Zeh: Why Bohm's Quantum Theory?, Found. Phys. Lett. 12 (1999) pp. 197-200, quant-ph/9812059v2
  7. ^ L. Vaidman: The Reality in Bohmian Quantum Mechanics or Can You Kill with an Empty Wave Bullet?, quant-ph/0312227 (submitted on 31 Dec 2003)
  8. ^ Born M. 1926, Z Phys. 38;803. Wave Mechanics
  9. ^ Solvay Conference, 1928, Electrons et Photons: Rapports et Discussions du Cinquieme Conseil de Physique tenu a Bruxelles du 24 au 29 Octobre 1927 sous les auspices de l'Institut International Physique Solvay.
  10. ^ von Neumann J. 1932, Mathematische Grundlagen der Quantenmechanik.
  11. ^ Bohm, David (1952). "A suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, I and II, Physical Review 85.
  12. ^ Bell, John S, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press
  13. ^ Y. Couder, A. Boudaoud, S. Protière, Julien Moukhtarb, E. Fort: Walking droplets: a form of wave-particle duality at macroscopic level? , DOI: 10.1051/epn/2010101, (PDF)

External links